La technique du double cadenas est purement théorique, et elle ne connais pas d'application pratique à ma connaissance... Vous pouvez télécharger ces documents au format pdf ici.
L'idée est d'imaginer un système n'utilisant pas de clefs privées communes qu'il faille se communiquer auparavant. Chacun utilisera son algorithme, sa clef…

En Théorie :

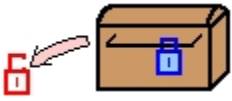
Le système est très simple. Alice et Bob vont choisir chacun un algorithme, que l'on symbolisera par un cadenas : Alice mettra son message dans un coffre, fermé par son cadenas, et elle enverra le tout à Bob :

Puis celui-ci y mettra son cadenas et renverra le coffre doublement cadenassé à Alice :

Alice retirera alors son cadenas et renverra une dernière fois le coffre à Bob :

Enfin Bob n'aura plus qu'à enlever le sien, ouvrir le coffre et lire le message.

La Difficulté :

Vu ainsi, le système à l'air assez simple et très facile d'utilisation, mais, d'un point de vu plus mathématique, on se heurte à une difficulté qui est la commutation des 2 algorithmes. En effet, en nommant f, la fonction utilisée par Alice, et g, celle de Bob, l'échange complet du message aura consisté à lui appliquer la fonction g^(-1) o f ^(-1) o g o f mais rien ne nous dit que l'on obtiendra finalement le message initial, c'est à dire que cette application est l'identité ! Il faut pour cela que les fonctions f et g commutent.
Or on a supposé qu'Alice et Bob n'ont pas communiqué entre eux auparavant. Il faut donc créer un catalogue de fonctions qui commutent, dans lequel les 2 interlocuteurs pourront piocher. D'un autre coté, il faut que ce catalogue soit suffisamment vaste, c'est à dire qu'il contienne un nombre de fonctions suffisamment grand, pour qu'un éventuel pirate n'ait pas trop de facilités à casser le code, par une attaque exhaustive, par exemple.

J'ai brièvement travaillé à trouver une application sans y parvenir, ni même trouver un système existant utilisant cette idée.

Exemple :

Un internaute, visiteur de ce site, ma gentillement contacté pour me faire part d'une remarque très judicieuse. Il existe une application simple à la méthode du double cadenas.
En effet les fonction Xor commutent ! Donc en reprennant nos personnages, Alice écrit son message et le crypte avec une clef de son choix dans une fonction Xor. Une excellente idée sera de choisir une clef aussi longue que le message, ce qui evitera tout cassage à partir de recherche de boucle. Ensuite elle transmet son message ainsi crypté à Bob qui fait de même. Il choisit une clef et applique un Xor sur le message reçu, avant de renvoyer le message obtenu à Alice. Elle applique alors de nouveau la même fonction, transmet une dernière fois le message à Bob, qui obtiendra le message décrypté après avoir lui aussi repassé son Xor avec la même clef.

On remarquera que dans ce cas, les fonctions f et g sont inversibles et leur propre inverse : f = f^(-1) et même chose pour g. Attention : je n'ai pas tenté de craqué un tel système. Il est peut être simple de casser ce code si on intercepte tous les messages transmis : f(m), g°f(m) et g(m).